排序
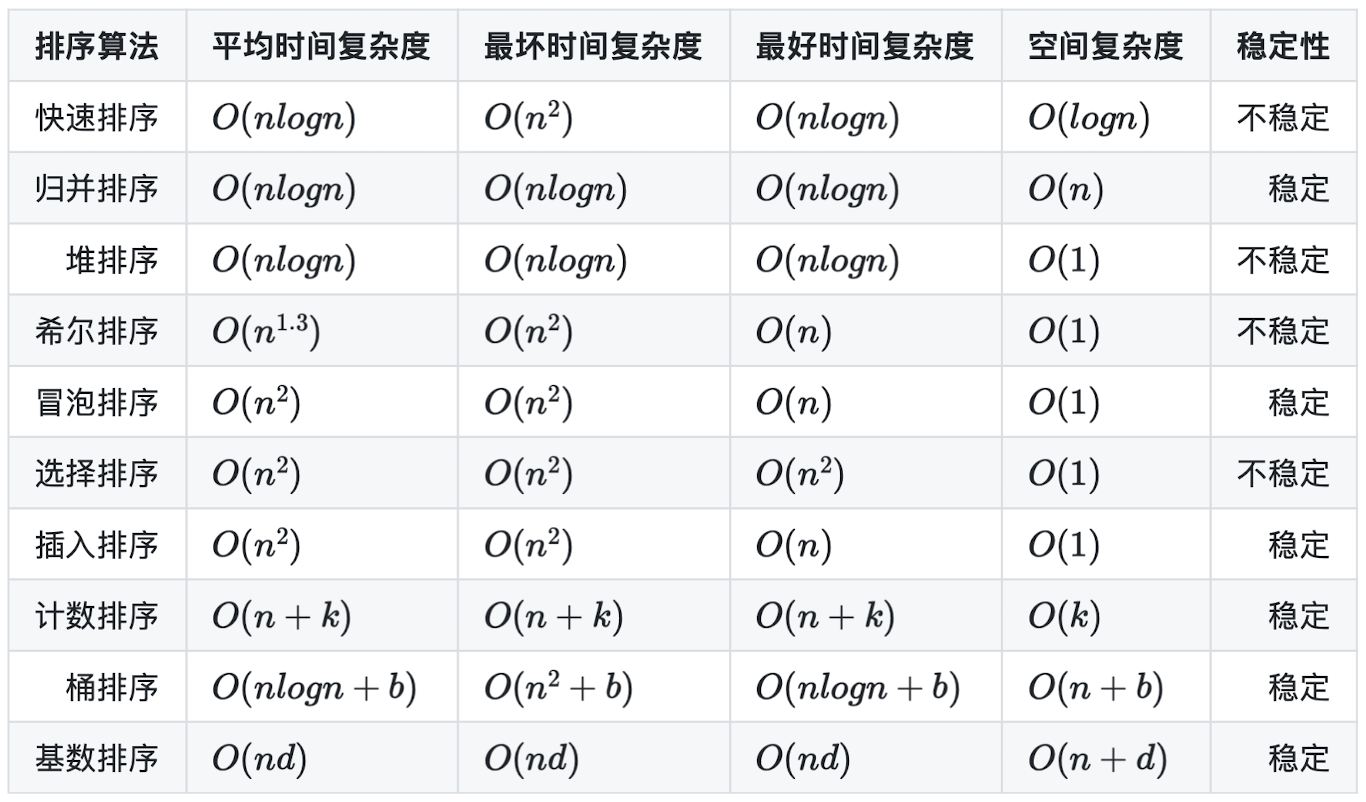
- 重点排序:快速排序 (不稳定),归并排序 (稳定),堆排序 (不稳定),希尔排序 (不稳定)
- 简单排序:冒泡排序 (稳定),选择排序 (不稳定),插入排序 (稳定)
- 有限数据范围,空间换时间:计数排序 (稳定),桶排序 (稳定),基数排序 (稳定)
快速排序
- 每次确定一个 pivot 的位置,左侧都比它小,右侧都比它大
- 从两边向中间遍历,直到不满足要求,则交换元素
- 稳定性:不稳定,两侧元素交换可能破坏稳定性
ts
function partition(nums: number[], lo: number, hi: number): number {
const randIdx = Math.floor(Math.random() * (hi - lo + 1)) + lo;
[nums[lo], nums[randIdx]] = [nums[randIdx], nums[lo]];
const pivot = nums[lo];
while (lo < hi) {
while (lo < hi && pivot <= nums[hi]) {
--hi;
}
nums[lo] = nums[hi];
while (lo < hi && nums[lo] <= pivot) {
++lo;
}
nums[hi] = nums[lo];
}
nums[lo] = pivot;
return lo;
}
function quickSort(nums: number[], lo: number, hi: number) {
if (lo >= hi) {
return;
}
const mi = partition(nums, lo, hi);
quickSort(nums, lo, mi - 1);
quickSort(nums, mi + 1, hi);
}
function sortArray(nums: number[]): number[] {
quickSort(nums, 0, nums.length - 1);
return nums;
}归并排序
- 合并两个有序数组只需要双指针、线性复杂度
- 不断分解子问题,直到数组只有一个元素、无需排序
- 稳定性:稳定,从左到右依次排列
ts
function merge(nums: number[], lo: number, mi: number, hi: number) {
const temp = new Array(hi - lo);
let i = lo;
let j = mi;
let k = 0;
while (i < mi && j < hi) {
if (nums[i] <= nums[j]) {
temp[k++] = nums[i++];
} else {
temp[k++] = nums[j++];
}
}
while (i < mi) {
temp[k++] = nums[i++];
}
while (j < hi) {
temp[k++] = nums[j++];
}
for (i = lo, k = 0; i < hi; ++i, ++k) {
nums[i] = temp[k];
}
}
function mergeSort(nums: number[], lo: number, hi: number) {
if (lo + 1 >= hi) {
return;
}
const mi = Math.floor((lo + hi) / 2);
mergeSort(nums, lo, mi);
mergeSort(nums, mi, hi);
merge(nums, lo, mi, hi);
}
function sortArray(nums: number[]): number[] {
mergeSort(nums, 0, nums.length);
return nums;
}堆排序
- 本质是堆上的选择排序
- 根据大顶堆的特性,最大的元素始终是第一个元素
- 构建大顶堆,从中间元素 (最后一个非叶节点) 到第一个元素 (根节点),依次向下调整
- 将最大的元素交换到末尾并排除出堆,然后向下调整,维持大顶堆的特性
- 稳定性:不稳定,首尾元素交换可能破坏稳定性
ts
function siftDown(nums: number[], lo: number, hi: number): void {
let parent = lo;
let child = parent * 2 + 1;
while (child <= hi) {
if (child + 1 <= hi && nums[child] < nums[child + 1]) {
++child;
}
if (nums[parent] >= nums[child]) {
return;
}
[nums[parent], nums[child]] = [nums[child], nums[parent]];
parent = child;
child = parent * 2 + 1;
}
}
function heapSort(nums: number[]): void {
const n = nums.length;
for (let i = Math.floor((n - 2) / 2); i >= 0; --i) {
siftDown(nums, i, n - 1);
}
for (let i = n - 1; i >= 0; --i) {
[nums[0], nums[i]] = [nums[i], nums[0]];
siftDown(nums, 0, i - 1);
}
}
function sortArray(nums: number[]): number[] {
heapSort(nums);
return nums;
}希尔排序
- 划定一个间隔,从 n / 2 到 1
- 每次排序只排序符合间隔的子序列,随着间隔缩小,数组逐渐有序
- 子序列内排序通常采用插入排序
- 稳定性:不稳定,不同子序列内的排序可能破坏稳定性
ts
function shellSort(nums: number[]) {
const n = nums.length;
for (let gap = Math.floor(n / 2); gap >= 1; gap = Math.floor(gap / 2)) {
for (let i = 0; i < gap; ++i) {
for (let j = i + gap; j < n; j += gap) {
const target = nums[j];
let k = j - gap;
while (k >= 0 && target < nums[k]) {
nums[k + gap] = nums[k];
k -= gap;
}
nums[k + gap] = target;
}
}
}
}
function sortArray(nums: number[]): number[] {
shellSort(nums);
return nums;
}冒泡排序
- 稳定性:稳定,从左到右依次冒泡
ts
function bubbleSort(nums: number[]) {
const n = nums.length;
for (let i = n; i >= 2; --i) {
let noSwap = true;
for (let j = 0; j < i - 1; ++j) {
if (nums[j] > nums[j + 1]) {
[nums[j], nums[j + 1]] = [nums[j + 1], nums[j]];
noSwap = false;
}
}
if (noSwap) {
break;
}
}
}
function sortArray(nums: number[]): number[] {
bubbleSort(nums);
return nums;
}选择排序
- 稳定性:不稳定,元素交换可能破坏稳定性
ts
function selectionSort(nums: number[]) {
const n = nums.length;
for (let i = n; i >= 2; --i) {
let maxIdx = 0;
for (let j = 0; j < i; ++j) {
if (nums[j] > nums[maxIdx]) {
maxIdx = j;
}
}
[nums[maxIdx], nums[i - 1]] = [nums[i - 1], nums[maxIdx]];
}
}
function sortArray(nums: number[]): number[] {
selectionSort(nums);
return nums;
}插入排序
- 稳定性:稳定,从左到右依次插入
ts
function insertionSort(nums: number[]) {
const n = nums.length;
for (let i = 1; i < n; ++i) {
const target = nums[i];
let j = i - 1;
while (j >= 0 && nums[j] > target) {
nums[j + 1] = nums[j];
--j;
}
nums[j + 1] = target;
}
}
function sortArray(nums: number[]): number[] {
insertionSort(nums);
return nums;
}计数排序
- 稳定性:稳定,从左到右依次处理
ts
function countingSort(nums: number[], minVal: number, maxVal: number) {
const count: number[] = new Array(maxVal - minVal + 1).fill(0);
for (const num of nums) {
count[num - minVal] += 1;
}
let idx = 0;
for (let i = minVal; i <= maxVal; ++i) {
while (count[i - minVal] > 0) {
nums[idx++] = i;
count[i - minVal] -= 1;
}
}
}
function sortArray(nums: number[]): number[] {
countingSort(nums, -50000, 50000);
return nums;
}桶排序
- 桶内排序算法:由于元素不多,可以使用简单的插入排序 (稳定),也可以使用高效的快速排序 (不稳定)
- 稳定性:如果按顺序放入桶内,且桶内排序是稳定的,则桶排序是稳定的
ts
function bucketSort(nums: number[]): void {
const n = nums.length;
if (n === 0) {
return;
}
const minVal = Math.min(...nums);
const maxVal = Math.max(...nums);
const bucketCount = Math.ceil((maxVal - minVal + 1) / n);
const buckets: number[][] = new Array(bucketCount).fill(0).map(() => []);
for (const num of nums) {
buckets[Math.floor((num - minVal) / n)].push(num);
}
let i = 0;
for (const bucket of buckets) {
bucket.sort((a, b) => a - b);
for (const num of bucket) {
nums[i++] = num;
}
}
}
function sortArray(nums: number[]): number[] {
bucketSort(nums);
return nums;
}基数排序
- 稳定性:稳定,按顺序放入桶中
ts
function radixSort(nums: number[], minVal: number, maxVal: number) {
let newMaxVal = maxVal - minVal;
let maxDigit = 0;
while (newMaxVal) {
maxDigit += 1;
newMaxVal = Math.floor(newMaxVal / 10);
}
const buckets: number[][] = new Array(10);
let div = 1;
for (let i = 0; i < maxDigit; ++i) {
for (let j = 0; j < 10; ++j) {
buckets[j] = [];
}
for (const num of nums) {
buckets[Math.floor((num - minVal) / div) % 10].push(num);
}
let idx = 0;
for (const bucket of buckets) {
for (const num of bucket) {
nums[idx++] = num;
}
}
div *= 10;
}
}
function sortArray(nums: number[]): number[] {
radixSort(nums, -50000, 50000);
return nums;
}